在量子計算和機器學習的快速發展背景下,量子數據壓縮和量子交叉熵技術的出現標志著量子機器學習領域的重要突破。這項技術不僅為量子數據壓縮提供了一種新的理論框架,也為量子機器學習算法提供了高效的損失函數。這一創新成果深刻改變了我們對量子計算和人工智能的理解,并且極大地推動了量子計算與現代數據科學的結合。
量子數據壓縮是量子信息學中的一項重要任務,其目標是通過量子算法減少數據的存儲空間,同時盡可能保持數據的完整性。量子數據的壓縮問題不同于經典數據壓縮,量子態的測量、相干性以及量子糾纏等特性使得這一過程更加復雜和具有挑戰性。
傳統的經典數據壓縮技術,如霍夫曼編碼或算術編碼,依賴于數據的冗余性和概率分布。然而,在量子計算中,數據的表示方式是量子比特(qubit),這使得數據的壓縮不僅涉及信息內容,還涉及量子態的相互作用。因此,量子數據壓縮不僅要求有效的算法,還需要一個深入的理論框架來指導實現。
量子交叉熵是量子信息學中的一個新興概念,它是經典交叉熵在量子環境中的擴展。在經典信息理論中,交叉熵被廣泛用作評估不同概率分布之間的差異。類似地,量子交叉熵則用于量化量子概率分布之間的差異,并在量子數據壓縮中扮演著至關重要的角色。
通過對量子交叉熵的最小值進行研究發現其與馮·諾依曼熵(von Neumann entropy)一致。這一發現不僅使量子交叉熵成為量子壓縮的自然選擇,也使其在量子數據壓縮中成為一個理想的壓縮率指標。馮·諾依曼熵本質上是量子態的不確定性度量,而量子交叉熵作為一種量化誤差的方法,為量子計算提供了對壓縮算法效率的深刻理解。
為了實現高效的量子數據壓縮,微云全息(NASDAQ: HOLO)提出了一種新型的量子數據壓縮協議。該協議基于可變長度編碼和量子強典型性原理,提供了一種通用的量子數據壓縮方法。可變長度編碼是一種經典的編碼技術,能夠根據符號的出現概率分配不同的比特長度。通過將這一思想引入量子環境,可以對量子數據進行更為精確和高效地編碼。
量子強典型性原理則指出,量子態在測量后會趨向一種“典型”狀態,且這種狀態的出現概率較大。結合這一原理,微云全息設計出一種量子數據壓縮機制,使得量子數據的編碼更加高效,并且符合量子信息的統計特性。通過對量子交叉熵和馮·諾依曼熵之間關系的深入理解,微云全息的協議能夠實現接近最優的壓縮率,減少冗余信息并保持量子數據的關鍵特征。
量子機器學習是量子計算與人工智能的結合,它利用量子計算的高速計算能力來解決傳統機器學習無法高效解決的問題。在量子機器學習中,損失函數的設計對于模型的訓練至關重要。經典的機器學習算法通常依賴于交叉熵損失函數來評估模型預測與實際標簽之間的差異,而量子機器學習則需要一種適合量子計算的損失函數。
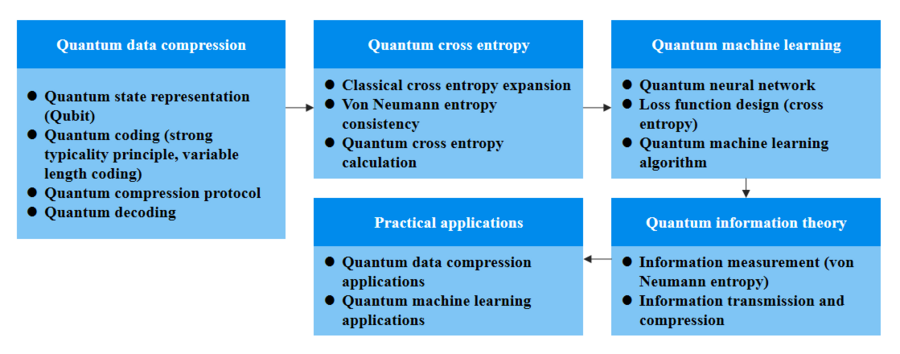
微云全息(NASDAQ: HOLO)提出的量子交叉熵恰好解決了這一問題。由于量子交叉熵能夠量化量子概率分布的差異,它非常適合作為量子機器學習中的損失函數。通過在量子神經網絡中使用量子交叉熵,可以有效地訓練量子模型,提高量子機器學習的性能。量子交叉熵作為損失函數的應用,不僅增強了量子機器學習算法的準確性,也進一步驗證了量子數據壓縮在量子計算中的廣泛應用。
量子交叉熵的最小值與馮·諾依曼熵的一致性為量子數據壓縮和量子機器學習提供了理論支撐。這一發現不僅加強了量子交叉熵在量子壓縮中的核心地位,也為量子機器學習的理論框架提供了重要的啟示。通過將量子交叉熵作為量子數據壓縮的關鍵指標,我們能夠更深入地理解量子信息的壓縮原理,并進一步推動量子機器學習領域的研究和應用。
量子交叉熵與馮·諾依曼熵的一致性表明,量子計算可以為數據壓縮和機器學習帶來革命性的變化。這一理論突破不僅擴展了量子計算在人工智能中的應用范圍,也為量子數據壓縮技術的實際應用提供了新的視角。通過量子交叉熵和量子壓縮技術的結合,量子機器學習將能夠實現更高效、更精確的算法,推動人工智能在各個領域的應用。
隨著量子技術的不斷進步,量子數據壓縮和量子交叉熵技術將在量子機器學習、量子通信、量子優化等多個領域發揮越來越重要的作用。相信,隨著這項技術的推廣,量子計算將在處理海量數據、加速模型訓練和優化算法等方面取得前所未有的成果。微云全息量子數據壓縮和量子交叉熵技術將可能成為量子計算領域的核心工具之一,為量子信息學和人工智能的融合發展開辟新的道路。期望,在不久的將來,量子機器學習能夠為解決全球性挑戰提供強大的技術支持,推動科技進步與社會發展。

來源:媒介聯盟
原標題:微云全息(NASDAQ: HOLO):量子數據壓縮與量子交叉熵,量子機器學習中的理論突破與應用前景







 廣告
廣告




 廣告
廣告

 廣告
廣告


